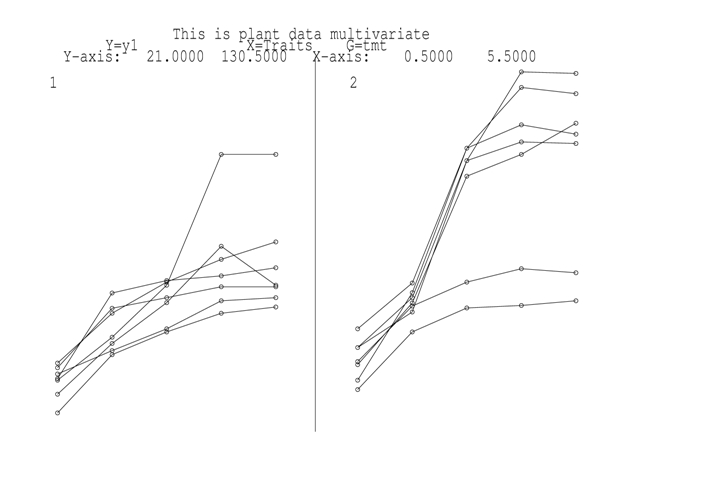
CORU:
σ2e = σ21+ σ22 and ρ = σ21/ (σ21+ σ22)
Portions of the two outputs are given below. The REML log-likelihoods for the two models are the same and it is easy to verify that the REML estimates of the variance parameters satisfy Eqn4, viz. σ2e= 286.310 which is about 159.858 + 126.528 = 286.386 and 159.858/286.386 = 0.558191.
#
# !r units
#
LogL=-204.593 S2= 224.61 60 df 0.1000 1.000
LogL=-201.233 S2= 186.52 60 df 0.2339 1.000
LogL=-198.453 S2= 155.09 60 df 0.4870 1.000
LogL=-197.041 S2= 133.85 60 df 0.9339 1.000
LogL=-196.881 S2= 127.56 60 df 1.204 1.000
LogL=-196.877 S2= 126.53 60 df 1.261 1.000
Final parameter values 1.2634 1.0000
Source Model terms Gamma Component Comp/SE % C
units 14 14 1.26342 159.858 2.11 0 P
Variance 70 60 1.00000 126.528 4.90 0 P
#
# CORU
#
1 LogL=-198.873 S2= 228.71 60 df 1.0000 0.3000
2 LogL=-197.950 S2= 234.83 60 df 1.0000 0.3667
3 LogL=-197.151 S2= 252.79 60 df 1.0000 0.4608
4 LogL=-196.878 S2= 284.06 60 df 1.0000 0.5531
5 LogL=-196.877 S2= 286.30 60 df 1.0000 0.5582
6 LogL=-196.877 S2= 286.31 60 df 1.0000 0.5582
Final parameter values 1.0000 0.5582
- - - Results from analysis of y1 y3 y5 y7 y10 - - -
Akaike Information Criterion 397.75 (assuming 2 parameters).
Bayesian Information Criterion 401.94
Model_Term Gamma Sigma Sigma/SE % C
units.coru(Trait) 70 effects
Residual SCA_V 70 1.000000 286.310 3.65 0 P
Trait COR_R 1 0.558191 0.558191 4.28 0 P
A more realistic model for repeated measures data would
allow the correlations to decrease as the lag increases such as occurs with
the first order
autoregressive model. However, since the heights are not measured at
equally spaced time points we use the EXP model. The
correlation function is given by
ρu= φu
where u is the time lag is weeks. The coding for this is
y1 y3 y5 y7 y10 ~ Trait tmt Tr.tmt residual units.exp(Trait !COORD 1 3 5 7 10 )Note that we need to supply the coordinates for the variables. A portion of the output is
LogL=-183.734 S2= 435.58 60 df 1.000 0.9500
LogL=-183.255 S2= 370.40 60 df 1.000 0.9388
LogL=-183.010 S2= 321.50 60 df 1.000 0.9260
LogL=-182.980 S2= 298.84 60 df 1.000 0.9179
LogL=-182.979 S2= 302.02 60 df 1.000 0.9192
Final parameter values 1.0000 0.91897
- - - Results from analysis of y1 y3 y5 y7 y10 - - -
Akaike Information Criterion 369.96 (assuming 2 parameters).
Bayesian Information Criterion 374.15
Model_Term Gamma Sigma Sigma/SE % C
units.exp(Trait) 70 effects
Residual SCA_V 70 1.000000 301.604 3.11 0 P
Trait EXP_P 1 0.918997 0.918997 29.50 0 P
When fitting power models be careful to ensure the scale of the
defining variate, here time, does not result in an estimate of
φ too close to 1. For example, use of days in this example would
result in an estimate for φ of about .993.
The residual plot from this analysis is presented in in the figure.
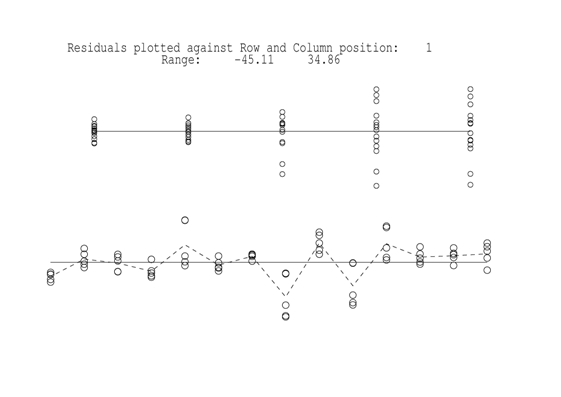
{Figure 2. Residual plots for the EXP variance model for the plant data. This suggests increasing variance over time. This can be modelled by using the EXPH model, which models Σ by Σ = D0.5CD0.5 where D is a diagonal matrix of variances and C is a correlation matrix with elements given by cij = φ|ti- tj|. The coding for this is
y1 y3 y5 y7 y10 ~ Trait tmt Tr.tmt residual units.exph(Trait !COORD 1 3 5 7 10 )Note that it is necessary to fix the scale parameter to 1 ( !SIGMAPAR) to ensure that the elements of D are identifiable. Abbreviated output from this analysis is
1 LogL=-195.598 S2= 1.0000 60 df : 1 components constrained
2 LogL=-179.036 S2= 1.0000 60 df
3 LogL=-175.483 S2= 1.0000 60 df
4 LogL=-173.128 S2= 1.0000 60 df
5 LogL=-171.980 S2= 1.0000 60 df
6 LogL=-171.615 S2= 1.0000 60 df
7 LogL=-171.527 S2= 1.0000 60 df
8 LogL=-171.504 S2= 1.0000 60 df
9 LogL=-171.498 S2= 1.0000 60 df
10 LogL=-171.496 S2= 1.0000 60 df
- - - Results from analysis of y1 y3 y5 y7 y10 - - -
Akaike Information Criterion 354.99 (assuming 6 parameters).
Bayesian Information Criterion 367.56
Model_Term Sigma Sigma Sigma/SE % C
units.exph(Trait) 70 effects
Trait EXP_P 1 0.906635 0.906635 21.79 0 P
Trait EXP_V 1 60.6454 60.6454 2.14 0 P
Trait EXP_V 2 73.3402 73.3402 1.98 0 P
Trait EXP_V 3 308.295 308.295 2.23 0 P
Trait EXP_V 4 434.744 434.744 2.53 0 P
Trait EXP_V 5 381.287 381.287 2.75 0 P
Covariance/Variance/Correlation Matrix Residual
60.50 0.8218 0.6753 0.5549 0.4134
54.80 73.51 0.8218 0.6753 0.5030
92.16 123.6 307.8 0.8218 0.6121
89.92 120.6 300.4 434.0 0.7449
62.74 84.15 209.6 302.8 380.7
Wald F statistics
Source of Variation DF F_inc
8 Trait 5 127.95
1 tmt 1 0.00
9 Tr.tmt 4 4.75
The last two models we fit are the antedependence model of order 1
and the unstructured model. These require, as starting values the
lower triangle of the full variance matrix. We use the REML estimate
of Σ from the heterogeneous power model shown in the
previous output. The antedependence model models Σ by the
inverse cholesky decomposition
Σ-1 = UDU'
where D is a diagonal matrix and U is a unit upper
triangular matrix. For an antedependence model of order q, then
uij = 0 for j>i+q-1. The antedependence model of order 1 has 9
parameters for these data, 5 in D and 4 in U. The input is given by
y1 y3 y5 y7 y10 ~ Trait tmt Tr.tmtThe abbreviated output file isunits.ante(Trait)
1 LogL=-171.501 S2= 1.0000 60 df
2 LogL=-170.097 S2= 1.0000 60 df
3 LogL=-166.085 S2= 1.0000 60 df
4 LogL=-161.335 S2= 1.0000 60 df
5 LogL=-160.407 S2= 1.0000 60 df
6 LogL=-160.370 S2= 1.0000 60 df
7 LogL=-160.369 S2= 1.0000 60 df
- - - Results from analysis of y1 y3 y5 y7 y10 - - -
Akaike Information Criterion 338.74 (assuming 9 parameters).
Bayesian Information Criterion 357.59
Model_Term Sigma Sigma Sigma/SE % C
units.ante(Trait) 70 effects
Trait ANTE_U 1 1 0.268753E-01 0.268753E-01 2.44 0 P
Trait ANTE_U 2 1 -0.628277 -0.628277 -2.56 0 P
Trait ANTE_U 2 2 0.372717E-01 0.372717E-01 2.41 0 P
Trait ANTE_U 3 2 -1.49128 -1.49128 -2.54 -1 P
Trait ANTE_U 3 3 0.599625E-02 0.599625E-02 2.43 0 P
Trait ANTE_U 4 3 -1.28095 -1.28095 -6.19 0 P
Trait ANTE_U 4 4 0.789625E-02 0.789625E-02 2.44 0 P
Trait ANTE_U 5 4 -0.967738 -0.967738 -15.40 0 P
Trait ANTE_U 5 5 0.390634E-01 0.390634E-01 2.45 0 P
Covariance/Variance/Correlation Matrix ANTE Residual
37.19 0.5946 0.3536 0.3102 0.3028
23.34 41.42 0.5946 0.5217 0.5092
34.66 61.51 258.4 0.8774 0.8563
44.38 78.77 330.9 550.4 0.9760
42.94 76.21 320.1 532.5 540.8
Wald F statistics
Source of Variation NumDF F-inc
8 Trait 5 189.36
1 tmt 1 4.19
9 Tr.tmt 4 3.91
The iterative sequence converged and the antedependence parameter
estimates are printed columnwise by time,
the column of U and the element of D. I.e.
D = diag( 0.0269 0.0373 0.0060 0.0079 0.0391 ),
U =
| 1.0 | -0.6284 | 0 | 0 | 0 |
| 0 | 1 | -1.4911 | 0 | 0 |
| 0 | 0 | 1 | -1.2804 | 0 |
| 0 | 0 | 0 | 1 | -0.9678 |
| 0 | 0 | 0 | 0 | 1 . |
Finally the input and output files for the unstructured model are presented below. The REML estimate of Σ from the ANTE model is used to provide starting values.
y1 y3 y5 y7 y10 ~ Trait tmt Tr.tmtThe antedependence model of order 1 is clearly more parsimonious than the unstructured model. The next Table presents the incremental Wald tests for each of the variance models. There is a surprising level of discrepancy between models for the Wald tests. The main effect of treatment is significant for the uniform, power and antedependence models. Table Summary of Wald test for fixed effects for variance models fitted to the plant dataunits.us(Trait) 1 LogL=-160.368 S2= 1.0000 60 df 2 LogL=-159.027 S2= 1.0000 60 df 3 LogL=-158.247 S2= 1.0000 60 df 4 LogL=-158.040 S2= 1.0000 60 df 5 LogL=-158.036 S2= 1.0000 60 df - - - Results from analysis of y1 y3 y5 y7 y10 - - - Akaike Information Criterion 346.07 (assuming 15 parameters). Bayesian Information Criterion 377.49 Model_Term Sigma Sigma Sigma/SE % C units.us(Trait) 70 effects Trait US_V 1 1 37.2262 37.2262 2.45 0 P Trait US_C 2 1 23.3935 23.3935 1.77 0 P Trait US_V 2 2 41.5195 41.5195 2.45 0 P Trait US_C 3 1 51.6524 51.6524 1.61 0 P Trait US_C 3 2 61.9169 61.9169 1.78 0 P Trait US_V 3 3 259.121 259.121 2.45 0 P Trait US_C 4 1 70.8113 70.8113 1.54 0 P Trait US_C 4 2 57.6146 57.6146 1.23 0 P Trait US_C 4 3 331.807 331.807 2.29 0 P Trait US_V 4 4 551.507 551.507 2.45 0 P Trait US_C 5 1 73.7857 73.7857 1.60 0 P Trait US_C 5 2 62.5691 62.5691 1.33 0 P Trait US_C 5 3 330.851 330.851 2.29 0 P Trait US_C 5 4 533.756 533.756 2.42 0 P Trait US_V 5 5 542.175 542.175 2.45 0 P Covariance/Variance/Correlation Matrix US Residual 37.23 0.5950 0.5259 0.4942 0.5194 23.39 41.52 0.5969 0.3807 0.4170 51.65 61.92 259.1 0.8777 0.8827 70.81 57.61 331.8 551.5 0.9761 73.79 62.57 330.9 533.8 542.2 Wald F statistics Source of Variation NumDF F-inc 8 Trait 5 196.02 1 tmt 1 1.72 9 Tr.tmt 4 4.46
| treatment | treatment.time | |
| model | (df=1) | (df=4) |
| Uniform | 9.41 | 5.10 |
| Power | 6.86 | 6.13 |
| Heterogeneous power | 0.00 | 4.81 |
| Antedependence (order 1) | 4.14 | 3.96 |
| Unstructured | 1.71 | 4.46 |